Pensamento xeométrico vs. pensamento aritmético

Co cambio de ano comezamos o bloque de Álxebra en 2º de ESO(5ª unidade didáctica do curso). Xa comentei que en 1º aproveitara a web Visual Patterns para introducir o estudo elemental das variables. É unha sorte que teñamos dispoñibles webs como esta, hai menos dunha década nin pensabamos na posibilidade, certamente.

Póñovos unha actividade desa web para que vexades de que estou a falar:

Pattern #14, from Katie, Squares in step 43 = 259

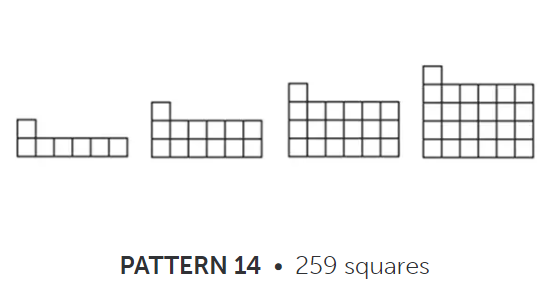
Cada viñeta da web contén os primeiros pasos dun patrón xeométrico, e o subtítulo inclúe o número da actividade, ás veces o autor e a resposta á pregunta implícita no patrón para o paso 43; neste caso, o número de cadrados que ten a figura n-ésima.

Neste exemplo, o razoamento parece claro: cada figura contén tantas ringleiras de 6 cadrados como o número do paso, máis un cadrado extra enriba. Por isto a fórmula que dá o número de cadrados no paso n é inmediata: 6n+1. A web proporciona o valor numérico para n=43 coa intención de que o alumno poida comprobar se a fórmula atopada funciona para un caso suficientemente grande para evitar o fenómeno da lei forte dos pequenos números.

A miña teima é que é habitual que os cativos non tenten razoar de xeito xeométrico. Probablemente sexa máis culpa miña debido a como introduzo as actividades que ás actividades per se, aínda así, coido que é comprensible que se dea este fenómeno. Cando un alumno observa un patrón, a tendencia natural fai que vexa algo así:

Paso	Nº de cadrados
1	7
2	13
3	19
4	25
...	...
n	?

E se o alumno ten boa base da aritmética de Primaria, pode chegar a ver que os números da columna da dereita non son máis que unha unidade por riba dos séxtuplos dos correspondentes da columna esquerda. A este pensamento é ao que me refería ao comezo co apelativo de aritmético, unha vez que se contan os cadrados das primeiras 4 figuras, un pode esquecer o patrón xeométrico e simplemente razoar sobre a secuencia numérica que obtivo.

Outro obstáculo é ben coñecido para os profesores de 3º de ESO: é moito máis sinxelo atopar a relación dunha figura do patrón coa figura anterior que a súa relación co lugar que ocupa no patrón, i.e, o paso. Na unidade de Progresións de 3º adoita suceder que os alumnos vexan rapidamente a diferenza das progresións aritméticas e máis adiante a relación de recorrencia, mais tarden en ver o termo xeral. Aínda por riba, a notación axeitada para as sucesións resulta difícil de dominar nesa etapa da aprendizaxe.


Vexamos outro exemplo desta mesma semana:

Pattern #3, Squares in step 43 = 990

Resulta obvio que este patrón é máis difícil, non si? O feito de que responda a unha progresión aritmética de orde 2, que no paso n o número de cadrados estea relacionado directamente con n+1  en troques de n e, por se fose pouco, que na fórmula haxa un denominador 2, complican a obtención da fórmula.

O bo que ten ser máis difícil é que non é inmediato recorrer ao razoamento puramente aritmético, pois en cada paso que avanzamos, a diferenza non é constante:

Paso	Nº de cadrados
1	3
2	6
3	10
4	15
...	...
n	?

Neste patrón tiven que axudar no encerado, resulta moi duro aínda traballando varios compañeiros xuntos. A axuda consistiu en mover as mans facendo espaventos para finalmente engadir uns cadrados difusos para o paso 2, como nesta imaxe:

   

Como contrapartida, é complicado chegar a atopar a fórmula sen razoar sobre a figura, que agora é máis claro que ten a metade de cadrados ca un rectángulo de base n+1 e altura n+2.

Seguirei utilizando este tipo de actividades, sen dúbida, mais non teño claro como facilitar o razoamento xeométrico sen que os patróns se pasen de dificultade. Tendo en conta ademais de que eu mesmo vexo antes habitualmente a fórmula a partir dos números(polo menos ata progresións aritméticas de orde 3) que a partir das figuras.

E vós que, traballades os visual patterns? Notastes este fenómeno ou é outra teima miña, outra para a colección?

Once

Atreveríame a afirmar que en todas as aulas nas que se dan criterios de divisibilidade, o criterio do 11 vai así:

Collemos o número que queremos saber se é múltiplo de 11, poñamos 49235.

Sumamos as cifras que ocupan un lugar impar, comezando pola dereita, neste caso:

4+2+5=11

Sumamos as cifras que ocupan un lugar par:

9+3=12

E restamos as dúas sumas anteriores: 12-11=1

Como o resultado non é múltiplo de 11, o número orixinal tampouco o é

Vexamos outro, 835032:

Lugar impar: 3+0+2=5

Lugar par: 8+5+3=16

16-5=11, que si é múltiplo de 11, polo que 835032 tamén.

Este algoritmo vén sendo o criterio tradicional de divisibilidade entre 11, polo menos en España.

E suscita varias cuestións:

A primeira: é algo habitual que haxa cativos que confundan a paridade do lugar das cifras coa propia paridade das cifras.

A segunda, que non será compartida por todos os profesores: non se pode explicar de xeito cabal por que funciona. A contorna na que mellor se entende é a da aritmética modular:

$10^{2k} \equiv 1 (mod 11)$ e $10^{2k+1} \equiv -1 (mod 11)$ (xunto co feito de que a equivalencia modular se leva ben coa suma... alguén dixo homomorfismo de grupos?)

Breve, elegante, fermoso... e inútil na aula.

Pois ben, hai outros criterios, que comparten a dificultade epistemolóxica mais sendo ben sinxelos de aplicar. Observade outro:

Separamos o número 49235 en grupos de dúas cifras, comezando pola dereita: 4-92-35

Sumamos estes números: 4+92+35=131

Repetimos ata ter un número de dúas cifras: 1-31, 1+31=32

Como o resultado final é un número de dúas cifras distintas(vaia, un que non é divisible entre 11), o número 49235 non é múltiplo de 11

Fagámolo co outro exemplo de antes: 835032

83+50+32=165, 1+65=66 si ten as dúas cifras iguais, polo que 835032 é múltiplo de 11.

A explicación con aritmética modular é igual de sinxela:

$10^{2k+1} \cdot a + 10^{2k} \cdot b \equiv 10a+b (mod 11)$

Pois ben, aínda hai outro criterio inmediato que é sinxelo de aplicar e que depara unha sorpresa. O mecanismo é moi simple, imos restando a última cifra ao número formado polo resto de cifras, ata chegar a unha única cifra. Probando con 49235:

4923-5=4918

491-8=483

48-3=45

4-5=-1

que non é múltiplo de 11, polo que 49235 non o era.

Fagámolo con 835032:

83503-2=83501

8350-1=8349

834-9=825

82-5=77

7-7=0

E polo tanto, 835032 si é múltiplo de 11

Sinxelo, non si?

Pero o mellor está por chegar. Mirade os números que fomos restando no procedemento, comezando por abaixo: 7, 5, 9, 1, 2

Osmades a punchline?

Pois si, amigos, 835032=11·75912

O procedemento non só informa sobre a divisibilidade entre 11, senón que ademais, dá o cociente. Dous polo prezo de un.

Chegados a este punto, teño que confesar que nunca expliquei outro criterio do 11 que non fose o tradicional, supoño que por pura preguiza; tería que comentalo no departamento e coido que xa teño sona de excéntrico abondo para meter en máis leas. Porque outra explicación non atopo.

O número 11, por outra banda, ten algunhas propiedades curiosas.

• É o maior número natural que non se pode expresar como suma de dous números compostos.

• É o único primo que ten lonxitude de período 2. É dicir, se divides entre 11 e non dá exacto, obtés dúas cifras no período, p.ex., $\frac{3}{11}=0,\widehat{27}$

• É o primeiro número primo p para o que $2^p-1$ non é primo ($2^{11}-1=2047=23 \cdot 89$)

• E algo máis provisional, é o número de anos que leva na rede Matemáticas na Rúa.