|
| Buscade abaixo o libro de David Wells para ver a relación coa Olimpíada do xoves |
Esta entrada leva sendo posposta varios anos, máis por esquecemento que por outra razón. Aproveitando que un xentil anónimo (aka ML) me lembrou este propósito, é hora de que comparta unha pequena listaxe de libros que, dun xeito ou outro, me teñen marcado como profesor. Nos tempos que vivimos é obvio que non son os libros os únicos referentes de formación que temos os docentes, mais nesta listaxe vou deixar fóra as webs, blogues, etc., referencias das que xa teño falado noutras entradas.
Por se alguén non está atento, hoxe toca falar de libros no sentido clásico do termo.
O labor docente na secundaria ten varios planos: por unha banda o profesor estudou na universidade unha carreira que lle proporcionou os coñecementos esenciais da súa disciplina, despois recibiu unhas directrices sobre pedagoxía (no extinto CAP ou no actual Máster de Secundaria). A estes planos é probable que de xeito autodidacta e paralelamente á práctica da súa profesión, sumase o coñecemento da didáctica da materia. Isto ten como consecuencia que nesta lista haxa varios apartados, aínda que omitín adrede os volumes sobre aspectos técnicos do ensino e a aprendizaxe.
Tentei engadir ligazóns aos textos completos onde foi posible, i.e., onde o big brother google deixa que aparezan. En calquera caso,
Library Genesis is your friend (este sería o meu lema se algún tarado me encomendase un curso de formación do profesorado novel).
Un último aviso: non podo asegurar que lese por completo todos os libros que van aparecer, sobre todo cos libros de consulta é difícil lembrar se un foi exhaustivo, ao non telos lido de xeito linear.
Antes de comezar, xa me estou a arrepentir dos que esquecín.
Matemáticas
Lino enteiro despois de rematar a carreira, cos meus prexuízos sobre o Cálculo Elemental xa asentados. Este volume ten dúas características positivas: fai reformular o que se sabe, e faino cun estilo moi elegante.
Este libro, xa demodé na disciplina, contén o que consideraban esencial desa disciplina dous dos mellores teóricos de números do momento. Ten un estilo por momentos austero.
Aínda que os dous libros son ben distintos en contidos e propósito, xúntoos acó porque grazas aos dous son un pouco menos ignorante en Xeometría. Coxeter foi un xeómetra formidable, e o seu dominio sobre a súa materia tradúcese ao seu estilo como autor.
O matemático que se pon sempre como exemplo de que se pode continuar traballando ata a senectude, Sierpinski fixo esta compilación de problemas, que na miña opinión forman parte da cultura matemática.
Este volume ten pouco que ver cos anteriores. Póñoo aquí porque pasei un verán resolvendo os problemas que contén, desde como calcular datas usando congruencias ata como resolver ecuacións diofánticas utilizando extensións cuadráticas dos números racionais. Cousas da xuventude.
Reflexión arredor das Matemáticas
Unha xoia de libro en todos os aspectos. Por poñer un exemplo, a análise que fai do Teorema Chinés dos Restos desde a súa orixe ata a formulación moderna abriume os ollos (btw, outro problema que podería ter aparecido na entrada
De que me soa a min isto?) Daquela vin mellor onde estaban algunhas ideas por embaixo da forma provisional que se lles dea. Algo semellante experimentei cando vin que a xeneralización de Euler do Teorema Pequeno de Fermat anunciaba punto por punto a demostración moderna do Teorema de Lagrange da Teoría de Grupos.
Aínda que vendo os contidos un podería pensar que é un tour de force das Matemáticas que se estudan na facultade, o certo é que os autores van deixando a súa opinión sobre a necesidade dos conceptos matemáticos e a súa posición dentro das Matemáticas como disciplina interconectada. Non é unha obra para ler nunha tarde.
A peculiar visión dun matemático peculiar, xa forma parte do folklore matemático a súa postura sobre a imprescindible estética das Matemáticas.
Unha delicia de libro. Consta de artigos independentes sobre temas moi variados, desde como crear movemento rectilíneo utilizando engrenaxes ata curvas de ancho constante ou o Problema de Waring.
Reflexión arredor do Ensino das Matemáticas
A
Sawyer mencioneino por
acó de pasada. Ide á web enlazada se queredes saber do seu labor docente. Eu estou namorado da súa intuición como profesor.
Deste
tamén falei xa.
Resolución de Problemas
Está pensado para o adestramento de olímpicos (
Arthur Engel foi moitos anos o capitán do equipo alemán da IMO) polo que cobre todos os temas que poden aparecer nunha olimpíada de alto nivel. Tendo isto claro, évos un compendio de matemáticas fermosas.
Semellante ao anterior, aínda que sen os problemas de maior dificultade. Tamén inclúe rudimentos de cálculo infinitesimal, xa que está máis dirixido a un concurso tipo Putnam que á IMO.
Tamén pensado como os anteriores, presenta os heurísticos tradicionais pero o rango de problemas cuberto é algo máis limitado.
Monos e cocos? Sombreiros que caen nun río? Calcetíns nun caixón? Unha viaxeira que colle un tren unha hora antes do habitual? Unha variedade inusitada de problemas é o que hai neste libro, polo que abrir unha páxina ao chou é un antídoto contra o aburrimento.
Fibonacci, Arquímedes, Euler, Gauss, Ramanujan, Steiner, Pascal,... atacaron problemas meramente lúdicos, polo menos na súa orixe. Petkovic fixo esta escolma milenaria.
A escolla de tres expertos problemistas. Non vou ser eu quen os emende.
Souben do termo "quicky" pasando pola sección de problemas do Mathematics Magazine que había na biblioteca da facultade, para min sempre estivo relacionado con Murray Klamkin, un dos autores do libro anterior. Máis tarde dei con este volume, do que teño tirado algún problemiña.
Outra selección de problemas, que coa visión de Soifer, ten certa querenza á combinatoria e aos xogos(idiosincrática dos matemáticos da antiga URSS)
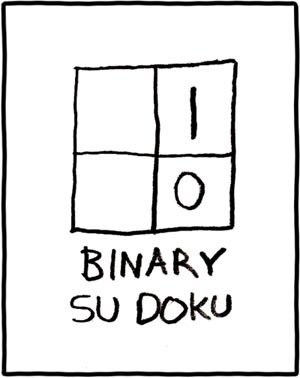
Wells é outro divulgador de primeiro nivel da nosa ciencia. Por poñer un exemplo de problema deste libro, observade a imaxe da cabeceira desta entrada. Tedes que cortar esa figura en dous cachos de tal xeito que se poidan unir para formar un rectángulo normal.
Só ten 21 problemas probabilísticos, pero vaia problemas!
Miscelánea
Outro clásico imprescindible, tan imprescindible que a última versión foi editada por Coxeter. Contén todas as Matemáticas recreativas que se coñecían a finais do século XIX, e tamén unha disquisición histórica sobre o Mathematical Tripos de Cambridge, que o lector poderá saltar sen remorsos.
Orixinalmente un curso de Donald Knuth en Stanford, Concrete Mathematics é a edición completada e mellorada daquel curso. O estilo non é o dos matemáticos puros, senón que está máis enfocado cara a manipulación e o cálculo.
Este libro pasoumo un amigo aínda estudando a carreira, que mercara a tradución ao castelán (lembranzas de antes dos tempos do pdf e o djvu). De lectura áxil, presenta a evolución da criptografía e da criptoloxía desde a antiga cifra César pasando pola máquina Enigma ata a actualidade.
Esta é unha elección obrigada. Se non o coñecedes aínda, correde, insensatos.
Un chisco de cultura popular, neste caso arredor dos xogos de azar, non vén mal entre tanta solemnidade. Haigh estuda o mundo das apostas, lotarías, xogos sinxelos,etc. desde o punto de vista da probabilidade.
Non é o único libro interesante do tristemente desaparecido Erickson, cuxo estilo é inconfundible. Neste volume presenta ao comezo de cada capítulo un feito rechamante. Por exemplo, no capítulo 8 atopamos:
"O número de triángulos non congruentes con lados enteiros e perímetro $10^{100}$ é 2083...3"(onde hai 196 treses)
Outro título enganoso: non esperedes unha colección de métodos da Matemática discreta, pois o que teredes entre mans recolle episodios históricos pasados pola peneira da intución e análise matemática. Entre eles, guerras, epidemias, Física,...
A referencia que temos todos ao saír da facultade. Ocupaba un lugar preeminente na bibliografía da materia optativa Historia das Matemáticas, que collín rematando a carreira. Quizais, para ampliar o inevitable eurocentrismo dunha obra como esta, sexa necesario complementar esta visión coa de
The Crest of the Peacock. Non-European roots of Mathematics, de George Gheverghese.
O título engana, pois en realidade é unha historia dos sistemas de numeración, comezando polo óso Ishango.
Seguro que achades de menos varios libros, non si? Moitos van agora:
Autores dos que tento(/tentei) ler todo o que atopo
- Lewis Carroll
- Henry Dudeney
- Martin Gardner
- Ron Honsberger
- Howard Eves
- Ian Stewart
- Alfred Posamentier
- George Polya
- Anthony Gardiner
- Claudi Alsina
- Miguel de Guzmán
- Richard K. Guy
- Titu Andreescu
- John Conway
- Adrián Paenza
- Edward Barbeau
Destes ides ter que buscar vós, que xa fartei de copiar links.
Nota mental: para todo o que lin, hai que ver o mal profesor que son.