24.12.23
(Outra vez) Problemas de Álxebra sen ecuacións
12.12.23
Outro aritgrama(máis)
Non sei en que andaba turrando, que me veu unha idea para un aritgrama, atopei unha solución, e velaquí:
 |
7.12.23
De ángulos e senos
No último exame de Matemáticas I puxen este exercicio:
Demostrar que a expresión $cos(\alpha+\beta)cos\beta+sen(\alpha+\beta)sen\beta $ non depende do valor de $\beta$
Habitualmente, cando poño cuestións de identidades trigonométricas en exames, tento que haxa varios camiños para atopar a demostración, para evitar frustracións alén das ordinarias. E este é un bo exemplo, pois é factible desenvolver todo o desenvolvible:
$$cos(\alpha+\beta)cos\beta+sen(\alpha+\beta)sen\beta=$$
$$(cos\alpha cos\beta-sen\alpha sen\beta)cos\beta+(sen\alpha cos\beta+cos\alpha sen \beta) sen \beta=$$
$$ cos\alpha cos^2 \beta- sen\alpha sen\beta cos\beta+sen\alpha cos\beta sen \beta+cos\alpha sen^2 \beta= $$
$$\\ cos\alpha cos^2 \beta+cos\alpha sen^2 \beta=cos\alpha(cos^2 \beta+ sen^2 \beta)=cos \alpha$$
que non depende de $\beta$, q.e.d.
Aínda que un profesor con algo de experiencia ou intuición saberá que o final da demostración dos alumnos vai ser algo distinta, utilizando a fórmula fundamental para substituír unha das razóns.
Mais tamén, como adiviñaría o avezado lector, hai unha proba nunha liña:
$$cos(\alpha+\beta)cos\beta+sen(\alpha+\beta)sen\beta=cos(\alpha+\beta-\beta)=cos\alpha$$
Que é máis complicado de ver por un alumno pola dependencia nos símbolos. Comprensible.
Buscando inspiración para o exame no libro Trigonometry de Gelfand & Saul, que é unha xoia, atopei este exercicio, que xa coñecía dalgunha outra fonte (pode que fose nun libro de texto antigo) pero esquecera. E tivo a consecuencia indesexada de facerme rememorar vellas ideas da carreira, en concreto a materia Elementos de Variable Complexa de 3º. A estrutura da expresión levoume á breve demostración que se vía aló das fórmulas para o seno e o coseno da suma e da resta de ángulos.
Pero antes, lembremos as demostracións habituais:
Seguramente a que aparece na maioría dos libros de texto se basee na figura seguinte:
 |
 |
$$\begin{pmatrix} cos\alpha & -sen\alpha \\ sen\alpha & cos\alpha\end{pmatrix} \cdot \begin{pmatrix} cos\beta & -sen\beta \\ sen\beta & cos\beta\end{pmatrix}$$
$$\begin{pmatrix} cos\alpha cos\beta-sen\alpha sen\beta & -(cos\alpha sen\beta + sen\alpha cos \beta) \\ sen\alpha cos\beta + cos\alpha sen \beta & -sen\alpha sen\beta+cos\alpha cos\beta\end{pmatrix}=\\ \begin{pmatrix} cos(\alpha+\beta) & -sen(\alpha+\beta) \\ sen(\alpha+\beta) & cos(\alpha+\beta)\end{pmatrix}$$
O lector hardcore deste blog lembrará que esta idea, formalmente, xa fixera aparición hai dez anos na entrada Matrices e Pitágoras?.
E aínda podemos exprimir máis o conto:
$$e^{i \alpha}\cdot e^{i \beta}=e^{i (\alpha+\beta)}$$
Utilizamos a fórmula de Euler e temos outra demostración ultrarrápida das fórmulas de adición.
Porén, o episodio que veu á miña memoria poñendo o exame non foi isto, senón a demostración que aparecía nun libro de texto da bibliografía de Elementos de Variable Complexa, que basicamente consistía no seguinte:
Consideremos $\omega \in \mathbb{C}$ e a función $f(z)=cosz cos(\omega -z)-senz sen(\omega - z)$
Calculamos a súa derivada:
$f'(z)=-senz cos(\omega-z)+cosz \cdot (-1) \cdot[-sen(\omega -z)]-cosz sen(\omega-z)- \\ senz \cdot (-1)cos(\omega -z)=-senz cos(\omega-z)+cosz sen(\omega -z)-cosz sen(\omega-z)+\\senz cos(\omega -z)=0$
Polo que a función é constante, e como $f(0)=cos\omega$, temos que: $$cosz cos(\omega -z)-senz sen(\omega - z)=cos \omega, \forall z \in \mathcal{C}$$, que é un xeito alternativo de escribir a fórmula para o coseno da suma de ángulos.
Un aspecto que distingue as diferentes probas é se son demostracións de comprobación ou de descubrimento. A última que amosei, alén de usar unha idea potente, só comproba algo xa coñecido, i.e., non serve para atopar a expresión; mentres que nas outras podemos atopar a expresión sen coñecela previamente.
Por outra banda, lembrades a demostración habitual da derivada do seno? Utiliza dúas cousas: o límite $\lim \limits_{x \to0}\frac{senx}{x}=1$ e, precisamente, o seno da suma na forma $sen(x+h)$. Sempre hai que ter coidado e traballar con xeito, non vaiamos demostrar o Teorema de Pitágoras vía o Teorema do Coseno.
26.11.23
Problemas elementais variados
Nos últimos días fun recollendo de diversas fontes problemas para os que non é necesaria a utilización de técnicas nin ferramentas sofisticadas, o cal non garante en absoluto que vaian resultar sinxelos.
Nun cuadrilátero ABCD marcamos os puntos medios dos lados BC e AD, M e N. Unimos M con A e D e N con B e C, e chamamos P á intersección dos segmentos AM e BN e Q á de MD e CN. O debuxo explica todo rapidamente:
 |
| Intúese o que hai que amosar? |
Por certo, estou case convencido de que compartín unha figura dun cuadrilátero moi semellante á anterior. Pero facendo as pescudas evidentes non a dou atopado no arquivo do blog, e mirar as case oitocentas cincuenta entradas...
Agora un de números:
Atopar dous números naturais distintos x e y que cumpran que $x+n$ é divisor de $y+n$ para $n=0,1,\dots,10$
Aviso: este problema reformula unha cuestión tan coñecida dos números naturais que xa practicamente é un tópico en divulgación, libros de problemas, etc. Pero hai que darlle unhas voltas á cabeza para ver por onde vai.
Veña, o seguinte é axeitado para preguntar nunha aula:
Amosar que se dous segmentos que miden o mesmo se intersecan xusto no punto medio, os 4 extremos son os vértices dun rectángulo.
 |
Imaxinade que nunha calculadora as únicas operacións dispoñibles son +, – e ²
Como argallaríades para atopar o produto de dous números, x e y?
Reparade en que non hai ningunha tecla para dividir entre dous.
E para rematar, un problema clásico que admite un feixe de aproximacións distintas na aula:
Atopa a suma dos ángulos internos dunha estrela de cinco puntas. Hai moitos xeitos distintos de atopala, a ver cantos dás feito.
 |
Xa tedes abondo para pensar nas avaliacións cando non funcione o xade.
18.11.23
Un xogo 3D de verdade
Unha das miñas vellas teimas consiste en anoxarme cando alguén fala de visión espacial cando realmente o único implicado na situación é a visión plana. Sendo consciente de que espacial pode referirse tamén ao plano, isto é algo superior a min. E esta teima esténdese ao ensino cando en actividades que supostamente avalían a visión espacial, o único razoamento imprescindible ten lugar no plano. E por último, tamén é habitual que no ámbito dos videoxogos tenten coar por xenuinamente 3D mecánicas que só utilizan vistas 3D, pero nas que o esencial, unha vez máis, é 2D.
Por iso levei unha grata sorpresa ao coñecer este xoguiño, Which Way Round?, no que a captura xa vos dará unha boa intuición da mecánica:
 |
A figura superior é xirada no plano paralelo ao chan, é introducida na caixa de tal xeito que deixa de verse, a caixa xira no espazo, e o xogador ten que escoller cal das opcións inferiores corresponde á nova orientación da figura. O xogo comeza sendo ben sinxelo, pero despois, ao compoñer varios xiros, estou certo de que vai poñer a proba a vosa memoria operativa, e, neste caso si que se cumpre, a vosa visión espacial. Probádeo e veredes.
28.10.23
Un problema inclasificable
Quen tiña unha hora libre e pensou "veña, vou mirar algún problema do Torneo das Cidades"?
Efectivamente, o voso amigo, que parece novato. Catorce anos pasaron desde a entrada Primeiro Problema dun Libro, dous desde Un Problema do Tournament of the Towns, un feixe desde que sei dos problemas para nenos de Vladimir I. Arnold, e nada, aínda non aprendín que achegarse de xeito inocente a problemas de competicións ou libros rusos nunca sae como un espera inicialmente.
En troques de compartir o problema co seu enunciado orixinal, fagamos unhas cantas liñas.
Partimos dunha circunferencia, que dividimos en oitavos do xeito habitual:
 |
 |
 |
 |
| Prometo que foi ao chou que saíse o diámetro vertical (total, só había 4 opcións) |
Probemos con outra numeración dos mesmos sectores:
 |
Podedes probar vós con calquera outra coloración e calquera outro xeito de numerar os sectores seguindo esas regras. Sempre ides obter dous semicírculos cos números do 1 ao 4.
Pero xa imaxinaredes que esta non é unha propiedade peculiar do 4. Podemos dividir o círculo en 16 sectores, e veremos que sucede o mesmo co número 8. Poñamos novamente un exemplo:
 |
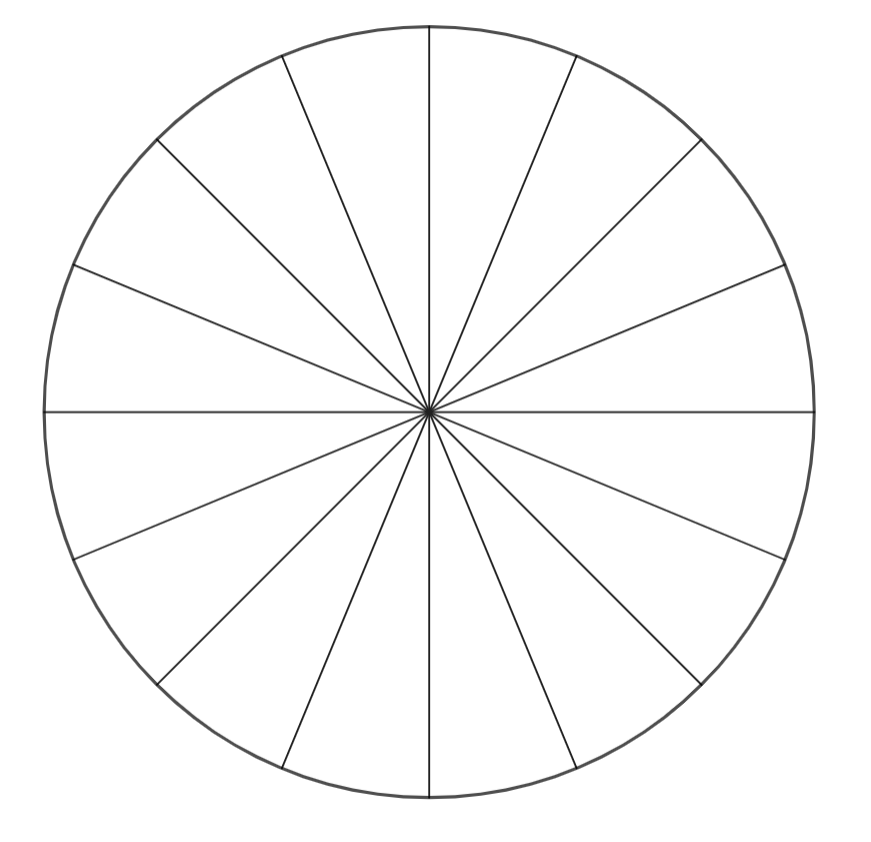 |
12.10.23
Uns problemas interesantes
Este comezo de curso vou a razón de 2 fichas novas por día de clase en 2º de ESO, co cal non tiven tempo para compartir as cousas interesantes que lin ultimamente. Aproveito esta véspera da ponte*, que pasarei cubrindo burocracia docente, para ordenar estas cuestións e problemas.
Comecemos por un problema que se presta a varios ataques, que vin nun libro de Alfred Posamentier. Sen dicir nada, xa o ides entender:
 |
Xa tedes para pasar a ponte.
*Ao final levoume ata a mañá do festivo.
21.9.23
Un método curioso que funciona(ás veces)
Cando traballamos a divisibilidade nas aulas de 1º de ESO habitualmente aparecen dous xeitos de calcular o máximo común divisor e o mínimo común múltiplo: por inspección dos divisores ou múltiplos dos números, ou mediante a descomposición factorial. Vexamos un exemplo con números xeitosos, 63 e 105.
$$D(63)=\{1, 3, 7, 9, 21, 63 \}$$
$$D(105)=\{1, 3, 5, 7, 15, 21, 35, 105 \}$$
Logo a simple vista o máximo común divisor é 21. Coa descomposición, $63=3^2 \cdot 7, 115=3 \cdot 5 \cdot 7$, xa sabedes o mantra, "os factores comúns elevados ao menor expoñente", $mcd(63,115)=3\cdot7=21$
Para o mínimo a inspección pode ser ben árida:
$$M(63)=\{63, 126, 189, 252, 315, 378, \dots \}$$
$$M(105)=\{105, 210, 315, 420, \dots \}$$
 |
 |
Co cal, hai que facer algún tipo de modificación ao método para que funcione nestes casos. Sinceramente, eu comento este método para dous números pero non para máis (ás veces si no caso do mcd). Imaxinades vós como arranxar o problema?
3.8.23
Outra demostración dun feito ben coñecido
Coido que xa falei aquí das demostracións habituais de que a suma dos ángulos internos de calquera triángulo plano é 180º, a saber:
1) Temos a que adoita vir nalgúns libros de texto, que utiliza o feito básico sobre ángulos nunha recta formados por rectas paralelas, que cunha imaxe estática queda claro:
Esta demostración é da que se pode facer unha comprobación pedindo aos alumnos que corten os ángulos en B e C e os poñan xunto a A.2) E temos a demostración "dinámica", que eu normalmente fago despois da anterior en 1º de ESO, botándolle teatro movéndome pola aula(supoño que como moitos de vós). Observade a figura de abaixo, e poñámonos, virtual ou fisicamente, no punto A mirando para B, andamos cara B, ao chegar aló xiramos para enfilar cara C, xiramos de novo para regresar a A, e finalmente en A, xiramos para poñernos mirando para B como ao comezo. Despois de tanto andar, simplemente estamos no punto de partida e na mesma posición, para o que tivemos que facer un xiro de 360º. E observando os ángulos de xiro, o que fixemos foi $180º-\widehat{B}+180º-\widehat{C}+180º-\widehat{A}=360º \rightarrow540- (\widehat{A}+\widehat{B}+\widehat{C})=360º \\\ \rightarrow 180º=\widehat{A}+\widehat{B}+\widehat{C}$ , q.e.d.
 |
| Collido de Resourceaholic/Gifs, descargado e subido por se o link está roto |
(Se un día teño tempo e ganas, tentarei facer un gif específico para un triángulo)
 |
| Aquí cansei de formatear triángulos para que quedasen bonitos |
De aquí deducimos que, chamando x á suma dos ángulos do triángulo:
16.7.23
Adiviña para mediados de xullo
Tiña varias ideas en mente para facer entradas, unha delas resolver a adiviña anterior, pero como xa saberedes todos, prefiro poñer problemas que as solucións. Polo que hoxe vai outra adiviña, esta máis sinxela. Que estades a ver nesta imaxe?
 |
Só un comentario: as 4 curvas non se solapan, estades a ver o anaco correspondente a cada unha.
26.6.23
Adiviña para rematar xuño
Botando unhas contas cheguei á fórmula que ides ver nun anaco. Mentres sigo con informes e memorias diversas, déixovos que pelexedes vós.
Se a e b son números reais positivos, que representará a expresión $\Large{\frac{8 ab \sqrt{ab}}{a+b}}$?
Boa sorte.
7.6.23
Un problema xeométrico do GCSE 2023
O de ter twitter provoca que, de vez en cando, saia algún hashtag á dereita que me chame a atención. Ultimamente vexo #maths con certa frecuencia, e cando dou no link, o habitual é que aparezan exercicios aritméticos e alxébricos do estilo dos de 3º de ESO. Pero tamén problemas tipo Sangaku, que se tes un anaco, adoitan ser ben divertidos.
Estes días non só andan os alumnos españois coa ABAU, tamén no Reino Unido están a celebrar o seu GCSE, e eu levo xa uns lustros remexendo en probas estandarizadas doutros países, é como un pracer culpable(aínda que a verdade é que teño tirado ideas de aí). E como sempre, comezan a aparecer queixas pola dificultade ou rareza dalgún exercicio. O deste ano, este problema co que seguramente os examinados non contaban:
 |
Se tentades resolvelo, axiña veredes que é moito máis sinxelo do que temían os rapaces.
6.6.23
Olimpíada Matemática Galega 2023-Fase Final-5
Chegamos ao derradeiro problema desta olimpíada, o único de xeometría:
Problema 5
Considera un hexágono regular de 4cm de lado. Unimos os puntos medios dos seus lados alternativamente tal como se indica na figura:
 |
- Cal é o perímetro do triángulo?
- Que proporción da área del é a área do triángulo?
 |
- Cal é o perímetro desta outra figura?
- Que proporción do hexágono é a área da figura?
4.6.23
Olimpíada Matemática Galega 2023-Fase Final-4
O cuarto problema, de combinatoria enumerativa:
Problema 4
O centurión Cayo Matemarius tiña ao seu cargo un grande número dos membros do exército lexionario de infantería de Gallaecia. Como era moi excéntrico, decidiu, para levar un control deles, asignarlle a cada un número capicúa. Averigua:
- Cantos capicúas hai de 2 cifras?
- Cantos capicúas hai de 3 cifras?
- Cantos capicúas hai de 4 cifras?
- Se en total hai 10.000 membros do exército en Gallaecia, cal é o maior capicúa que se utilizará?
Nota: Un número capicúa é aquel que se le igual de dereita a esquerda que de esquerda a dereita, sen contar os que comecen por cero.
Os tres primeiros apartados son os típicos que uso nas aulas de 1º de ESO cando traballamos o sistema de numeración, para ir metendo algo de razoamento. O cuarto apartado xa é máis bonito e requira un chisco máis de reflexión.
Porén, considero que nesta fase final houbo demasiados problemas "de números". Como é tradicional, o 5º problema non vai ser deste estilo.
3.6.23
Olimpíada Matemática Galega 2023-Fase Final-3
O terceiro problema desta fase final é un coñecido exercicio de matemáticas recreativas, o de atopar un número autodescritivo:
Problema 3
Ada é unha rapaza moi organizada e sempre que ten que inventar un contrasinal para unha nova aplicación escribe un número que sexa doado de recordar por ela, seguindo algunha propiedade interesante. Neste caso, o contrasinal que utilizou para a aula virtual deste curso ten as seguintes características:
- É un número de dez díxitos.
- O primeiro díxito é igual á cantidade de ceros do contrasinal.
- O segundo díxito é igual á cantidade de uns.
- O terceiro revela a cantidade de douses.
- E así sucesivamente, ata o décimo díxito, que indica a cantidade de noves.
Saberías obter o contrasinal de Ada?
É unha verdadeira mágoa coñecer o problema xa e non poder desfrutar de atopar a solución.
2.6.23
Olimpíada Matemática Galega 2023-Fase Final-2
Imos co 2º problema desta fase final.
Un exercicio previo podería ser adiviñar que hai que facer coa táboa de abaixo sen ler o enunciado. Premio á perspicacia a quen dea feito.
Problema 2
Na Casa dos Mosaicos atópase o mosaico da figura. A arqueóloga do Concello estima que se trata do código de entrada a unha irmandade segreda, forofa do número 126. Cre que se debería poder completar obtendo os divisores do dito número e, posteriormente, completando os ocos de forma que sumen o que indica cada fila e columna. Podes axudarlle?
 |
1.6.23
Olimpíada Matemática Galega 2023-Fase Final
Non tiña pensado comentar os problemas da fase final da Olimpíada deste ano, mais cambiei de opinión ao ver o 1º(quizais tivo algo que ver tamén que aínda rematei as clases de 2º de BAC este martes, quen sabe).
Comparto:
Problema 1
Nun instituto de Lugo matriculáronse no presente curso escolar un 10% máis de estudantes que o ano pasado. O número de rapaces aumentou un 5% e o de rapazas un 20%.
a) Que proporción de rapazas había no dito centro educativo o curso pasado?
b) Que proporción de rapaces hai no presente curso escolar?
Non sei se escribín algunha vez que me encanta este tipo de problemas nos que hai máis dunha variable e nas que o que se pide non é ningunha das variables, senón unha relación entre elas, habitualmente a razón. Como proba deixo por aquí problema do historial do blog:
Da entrada Problems for the Million, Nun parque só hai gatos de dúas cores: brancos e negros. Os gatos machos representan o 55% do total de gatos do parque. A proporción entre machos brancos e machos negros é igual á proporción entre gatos brancos e gatos negros. Achar a proporción entre machos brancos e femias brancas.
Na entrada Traballos de Álxebra podedes atopar o dos gatos que pensan que son cans e os cans que pensan que son gatos, se o lestes saberedes sen dúbida cal era.
Sobre o problema da olimpíada, é posible modificar os datos dados ou a pregunta final para dar lugar a problemas semellantes pero distintos. O primeiro que se me ocorre é que, en troques de dar o aumento de rapaces e rapazas, poderíamos indicar como varía a proporción de rapazas respecto ao total(e por tanto a de rapaces), ou dar a proporción final, e preguntar pola variación porcentual de cada grupo.
Por outra banda, credes que moitos alumnos notarían que se os rapaces aumentan un 5% e as rapazas un 20%, pero o aumento global é do 10%... entón ten que haber o dobre de rapaces que de rapazas, sen facer álxebra ningunha? (Disto falei na entrada Exercicios tan malos que son bos)
Un problema ben fermoso, que se pode utilizar como enriquecemento nas aulas, na miña opinión.
10.5.23
SineRider
Había tempo que non vía un xogo matemático on line con certa solidez, e lendo feeds atopei Sinerider, cuxo nome dá unha pista se xa coñecíades o vello Linerider, no que había que debuxar liñas a man alzada para que un trineo chegase a un obxectivo. Pois ben, observade unha das pantallas iniciais do xogo e xa ides adiviñar de que vai:
 |
O xogo ten un mapa no que avanzamos seguindo camiños. Reparade neste título, por exemplo:
 |
| Do sementador? |
Como adiviñastes, o xogo vai de escribir a expresión alxébrica dunha función para que o fantasma protagonista do xogo esvare pola súa gráfica. Mais ten varias innovacións con respecto aos distintos avatares desta idea que levo vendo lustros: a que vin que máis me encheu o ollo foi a de poder incluír a variable temporal na función que escribas, co cal ademais de que o fantasma esvare sobre a gráfica, esta variará simultaneamente. E nalgunhas pantallas é máis difícil do que parece cadrar isto para acadar o obxectivo, que ás veces consiste en que o fantasma pase por unhas letras en orde, noutros mover co noso protagonista un círculo por unha especie de correa, etc.
Ademais deste xogo-aventura, os autores crearon un bot en twitter que está a compartir retos, non sei ben con que frecuencia. Observade un chío de hoxe:
Sinerider Daily Puzzle #21 - This one is absolutely incredible, just wait, you'll see! https://t.co/S6wmZnRWaq
— SineRiderBot (@SineRiderBot) May 8, 2023
E hai un subreddit, SineRider, no que a xente comenta as dificultades e solucións dos retos.
Como dato curioso, o colectivo que creou o xogo, Hack Club, seica está formado por miles de mozos programadores do mundo.
7.5.23
Aproveitando un problema estándar
Creo que xa comentei que este ano dou dúas aulas de 1º de ESO, que por tanto segue a ser o curso que máis veces dei nos case vinte anos que levo no choio(isto lembra a un problema clásico de TIMSS, a ver se o atopo1). E aínda que a LOMLOE viña coa pretensión de reducir o número de contidos, o certo é que aínda temos máis cousas que dar, ao incluír o pensamento computacional no sentido alxébrico. Cousa que, non é por botar flores, xa vaticinara eu hai tres anos:
, na práctica, leve a ENGADIR CONTIDOS. E a proposta que acabo de ler que conecta as Matemáticas e a Informática, https://t.co/FhY372Pfu1, é un caso claro. Case todo soa ben(hai moito que roer no que din sobre modelización) pero, alguén cre que a Administración adoptaría unha 2/5
— J.J. Rodríguez (@jjcanido) June 10, 2020
Isto, sumado a outros factores, leva a que en maio estea aínda no sentido alxébrico, botando contas de cantas cousas importantes non van ver. E iso que, sendo rigoroso, non estou a cumprir co espírito da avaliación LOMLOE, porque como xa expliquei en varias ocasións, é unha trangallada que non permite determinar o que sabe facer un alumno.
E hoxe tocou resolver problemas co método alxébrico, para o que usei o libro de texto que tiven que escoller eu, cando a miña opción era non ter libro de texto. Cousas da vida.
O anódino problema do libro dicía algo así como:
Atopa dous números cuxa suma é 241 e cuxa diferenza é 27.
Expliqueilles eu como resolvelo de varios xeitos. Os dous evidentes a este nivel:
- Utilizando a diferenza para determinar as incógnitas, a e a+27, e logo usando a condición sobre a suma para establecer a ecuación
- Utilizando a suma para determinar as incógnitas, b e 245-b, e logo usando a condición sobre a diferenza para establecer a ecuación.
| 1º número | 2º número | Suma | Diferenza |
| 134 | 107 | 241 | 27 |
| 10 | 4 | ||
| 43 | 13 | ||
| 26 | 26 | ||
| 16 | 6 |
E pedín que completasen eles as outras. E para moitos non foi, nin de lonxe, inmediato. Agás un cativo, que resolvera o problema orixinal sen álxebra, que o fixo rapidísimo.
| 1º número | 2º número | Suma | Diferenza |
| 134 | 107 | 241 | 27 |
| 7 | 3 | 10 | 4 |
| 28 | 15 | 43 | 13 |
| 26 | 0 | 26 | 26 |
| 11 | 5 | 16 | 6 |
 |
Figura non feita a escala, bla, bla, bla... |
 |
Onde collín o cacho azul de abaixo da 1ª figura e leveino a continuación da parte de arriba, co cal temos dúas veces seguidas o 1º número.
1 Ah, atopei o ítem de TIMSS, é este do grao 8 de 1995:
P5. Tres quintos dos estudantes dunha clase son rapazas. Se 5 rapazas e 5 rapaces son engadidos á clase, cal das seguintes afirmacións é certa?
2.5.23
Olimpíada Matemática Galega 2023-Fase Local-5
Rematamos a quenda da fase local deste ano cun fermoso problema métrico:
Problema 5
Calcula a área da zona sombreada sabendo que ABCD é un cadrado de lado 1 m e os triángulos ACE e ACF son equiláteros iguais.
 |
 |
| Os lados dos cadrados medían 7 cm e 2 cm, e os seus lados eran paralelos |
1.5.23
Olimpíada Matemática Galega 2023-Fase Local-4
No cuarto problema desta fase local vaticino que non vos vai facer falta ler o enunciado:
Problema 4
A veciñanza dunha aldea deseñou a seguinte distribución das leiras das que dispoñen para dedicalas ao cultivo de produtos autóctonos. Desexan utilizar o mínimo número de produtos diferentes e colocalos de tal forma que en cada parcela se colleite un produto diferente a todas as que lindan con ela. Cal é o número mínimo de produtos que precisan?
 |
Perdoade a foto mal tirada, por sorte o problema non é métrico senón topolóxico.
O problema consta de dúas partes: primeiro amosar cantas cores, perdón, cultivos, son necesarios, e logo amosar que son suficientes, i.e., que para ese número necesario é posible atopar unha configuración. Esta sutileza témome que sexa excesiva para unha solución completa. Imaxino que o que máis se verá nas respostas é un xeito correcto de encher a figura sen razoar por que non pode facerse con menos cultivos. Veremos.
30.4.23
Olimpíada Matemática Galega 2023-Fase Local-3
 |
Imos co seguinte e controvertido problema da Fase Local da Olimpíada deste ano:
Problema 3
Cantos anos do Século XXI verifican a propiedade de que dividindo o número do ano por 2, 3, 5 e 7 obtemos sempre de resto 1?
Observación: Considérase que o Século XXI comezou o 1 de xaneiro de 2001.
Cualifiqueino de controvertido porque cando un resolve o problema observa que non hai ningún ano neste século que cumpra as condicións. E seguramente haberá cativos que o resolvan e dubiden ao ver que non hai ningunha solución. O primeiro que pensei eu na sesión foi que trabucaran século con milenio, sinceramente.
Por outra banda, o problema é clásico, e variantes del aparecen nalgúns libros de texto. Non lembro en que editorial pero xuraría que vin ata a variante "atopa o menor número que dividido entre 2 deixa resto 1, dividido entre 3 deixa resto 2, entre 4 deixa resto 3, etc."
O meu veredito, aínda así, é que o problema é axeitado para esta fase. O feito de que non haxa solucións pode servir para amosar destreza nas explicacións, que entre cativos de bo desempeño todo hai que usar para distinguir os mellores.
29.4.23
Olimpíada Matemática Galega 2023-Fase Local-2
Seguimos a xeira da fase local co segundo problema:
Problema 2
Letras diferentes representan cifras diferentes e letras iguais representan a unha mesma cifra ou o mesmo valor.
Sabendo que S=2, obtén que cifra se corresponde con cada letra na expresión e se hai unha ou varias solucións ao problema:
 |
P.S.: como no caso da Carta Roubada, de Poe, hai algo a simple vista que dá algo de... non sei como denominalo...
28.4.23
Olimpíada Matemática Galega 2023-Fase Local
 |
Onte, xoves 27, celebrouse a fase local da Olimpíada Galega de 2º de ESO, cuxa sede en Ferrol é o IES Canido desde hai 6 anos. A Olimpíada é organizada por compañeiros de Lugo de Agapema, a Asociación Galega do Profesorado de Educación Matemática, á que pertenzo (non hai moito) aínda que eu manteña opinións claramente diverxentes en cuestións esenciais da ensinanza das Matemáticas, como saberedes se ledes isto ou o meu twitter hai tempo.
Como outros anos, procedo a compartir os problemas que caeron nesta fase, pois considero que sempre se lles poder dar un uso nas aulas, senón como actividades ordinarias (non sempre), desde logo como actividades de enriquecemento.
Problema 1
Nun saco botamos bólas brancas, bólas negras, dados brancos e dados negros. O 20% dos obxectos do saco son dados e o 40% das bólas son brancas. Se en total hai 300 obxectos:
- Cantos deles son bólas?
- Cantos son bólas negras?
- Sabendo que o 60% dos obxectos son negros, que porcentaxe hai de dados brancos?
Translate
Interesante
-
-
Geology MurderHai un día
-
-
Cantos goles se marcan no fútbolHai 3 semanas
-
-
-
-
-
muller e matemáticaHai 7 anos
-
It Never Stops with PythagorasHai 7 anos
-
-














