Para sabelo, podes probar con este problema que teñen que facer os meus alumnos de 1º B para o mércores (os datos tirados da edición on line de El País, o das 14 pagas inventeino eu):
O salario anual do Gobernador do Banco de España será recortado un15%, quedando en 165.000 €.
Cal é o seu salario mensual actualmente, se cobra 14 pagas?
Curiosamente os alumnos de cursos superiores tenden a resolver estes problemas utilizando ecuacións, cando non é necesario. Nós estudamos ecuacións en 1º de E.S.O. antes que proporcionalidade e porcentaxes, pero cambiar a orde non suporía ningún atranco.
Por certo, non é o primeiro problema deste estilo que facemos. A técnica necesita ser explicada, e tamén practicada. A única directriz que lles dou despois de adestralos nun par de problemas é: "Se alguén calcula o 15 % de 165000, córtolle as mans". Instrucións claras, ante todo.
Para rematar, e por se resultades saber menos que un neno de 1º, podedes ver que tal vos vai neste xogo de habilidade (algunhas bastante estúpidas, máis ben de velocidade):
Skill Test
25.5.10
Martin Gardner
Quizais para moitos non signifique nada este nome. Pero para os seus seguidores, coma min, que lemos libros como os Entertaining Mathematical Puzzles, Mathematical Circus (tradución ao español on line, Circo Matemático), e tantos outros, Martin Gardner forma parte da nosa cultura, non só matemática, senón cientifica en xeral. Por poñer un exemplo, a primeira vez que lin sobre a Faixa de Moebius (que era o meu anterior avatar neste blog) foi nun libro de Gardner, varios anos antes de estudala formalmente en Topoloxía Xeral de 2º da carreira.

Pois ben, o maior divulgador do século XX finou o sábado aos 95 anos. Ademais da divulgación matemática, Gardner concentrou os seus esforzos en loitar contra os fraudes pseudocientíficos. Fraudes que non deixan de ameazarnos hoxe en día: non hai máis que botarlle unha ollada á televisión, non só a anuncios fraudulentos sobre falsas propiedades de "produtos máxicos", senón tamén Power Balance e outras trapalladas... Con este fin foi un dos fundadores do Committee for the Scientific Investigation of Claims of the Paranormal e escribiu unha columna no Skeptical Inquirer desde 1983 ata 2002.
Para homenaxealo hoxe proporei un par de problemas tirados dun dos seus libros:
Mr. Smith ten pensado viaxar en coche de Chicago a Detroit, e despois volver polo
mesmo camiño. Quere ter unha velocidade media de 60 millas por hora en toda a viaxe. Ao chegar a Detroit calculou a súa velocidade media na viaxe de ida e observou que foi só de 30 millas por hora. A que velocidade media ten que facer a viaxe de volta para que a súa velocidade media de toda a viaxe sexa a desexada, é dicir, 60 millas por hora?
Calcula a diagonal do rectángulo, da figura, coa única axuda das dúas medidas que aparecen:

Podedes var un artigo sobre Gardner en El País.
Etiquetas:
Matemáticos,
Problemas,
Xeometría
21.5.10
Difícil ou moi difícil?
O xoves estaba eu un pouco parvo, o que provocou que un simulacro de exame que ía darlles aos alumnos de 3º quedase no rango de simulacro de simulacro. O exame foi hoxe venres, polo que pensei en utilizar o simulacro directamente como exame. Pero debido a que non son totalmente maligno (iso déixoo para 2º de E.S.O. B), e a que os simulacros adoitan ser moito máis difíciles que os exames, pois déronme as doce pensando problemas onde utilizar o Teorema de Pitágoras. Comparade vós mesmos o problema que estaba no simulacro, que xa utilicei varias veces (a última no 2008-09 nun boletín de exercicios de ecuacións de 4º):
 Nesta figura hai que atopar o valor do raio da circunferencia azul (non vai ser o da verde).
Nesta figura hai que atopar o valor do raio da circunferencia azul (non vai ser o da verde).E agora o problema que finalmente apareceu no exame:
 Onde hai que calcular a área da zona violeta, sabendo só que o lado do cadrado verde é 5 cm.
Onde hai que calcular a área da zona violeta, sabendo só que o lado do cadrado verde é 5 cm.Se algún alumno meu de 3º C le este post (cousas máis raras teño visto), quizais modifique a súa opinión sobre a dificultade do exame. Quizais.
Ben, e cambiando totalmente de tema, o meu compañeiro José Luis colgou no seu blog os audios das pasaxes da Historia que narraba maxistralmente o xornalista Juan Luis Cebrián. Se non escoitastes nunca unha, aquí tedes a oportunidade.
17.5.10
No Día das Letras Galegas
Aínda non entendo a razón de que sexa festivo, pero ben, non me vou queixar deste luns ocioso e na casa.
Había tempo que non atopaba un xogo sinxelo de aprender e que fose adictivo ao estilo do Bloxorz, o Tilox, o 3D Logic, ou , neste ano, o Continuity. En Passion for Puzzles, como tantas outras veces, atopei este xogo, Gravit-Eye, que incide na idea da manipulación da gravidade para chegar a un obxectivo. Só xoguei unha partida, e podo dicir que hai fases nas que hai que pensar bastante para chegar á solución.
Observade unha captura da fase 17, por poñer un exemplo:
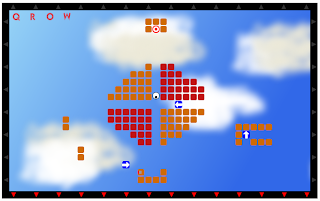
Para mover o "ollo" hai que utilizar as frechas e X para saltar. Máis sinxelo, imposible (non exactamente, probade Canabalt e veredes).
Se non vistes o seguinte vídeo (saíu en varios blogs recoñecidos, eu vino en Boing Boing), botádelle un ollo. É ben interesante:
15.5.10
The knight's tour
Ben, como dixen no anterior post, vou presentar a solución de Euler ao problema do cabalo de xadrez. Pero antes, unha solución que calquera de nós podería atopar (por exemplo, naquelas longas horas de 3º de B.U.P. nas que me ensinou o problema o meu compañeiro de clase, hai xa 17 anos-non todo era xogar aos "ceros"):

Ben, esta volta do cabalo (moito máis bonito en inglés o nome, por certo) non ten nada de particular. A ver se observades o que ten de extraordinaria a solución de Euler:

É boa idea seguir o camiño do cabalo, se o facedes veredes rapidamente o quid da cuestión.
Etiquetas:
Matemáticos,
Problemas
12.5.10
Euler, o xenio prolífico
No anterior post apareceu unha pequena mostra da capacidade e vista matemáticas do grande matemático Leonhard Euler. En concreto, a elaboración dun cadrado máxico 4x4 onde tódalas entradas eran cadrados perfectos. Pero isto non é máis que o comezo: Euler é o matemático máis prolífico da historia. As súas obras completas ocuparían entre 60 e 80 volumes, e os seus intereses cubrían tódalas ramas das Matemáticas e a Física: xeometría, análise, álxebra, astronomía... ata creou disciplinas novas! Un dos problemas clásicos das Matemáticas recreativas, o Problema das Pontes de Königsberg foi resolto por Euler, dando lugar a unha das materias máis entretidas, elegantes e sorprendentes das Matemáticas: a Topoloxía. Sen entrar en detalles, observade que a disposición física dos nodos dunha rede de ordenadores chámase topoloxía de rede.
Pero ao nivel que podo comentar neste blog, Euler foi tamén formidable á hora de resolver problemas, tanto "serios" como "lúdicos". É enorme a cantidade de problemas famosos, xogos e paradoxos que foron resoltos por Euler. Antes de comentar algúns, tentade vós resolver un problema dos que tratou este magnífico matemático. Non sei se xa o comentei aquí, pois ás veces mesturo os temas tratados nas aulas e os temas dos que escribo aquí. E nalgunhas clases deste ano do ano pasado si que apareceu o problema. Ao choio:
Movendo ao xeito dun cabalo de xadrez, e comezando nunha cela calquera do taboleiro, tenta pasar por tódalas celas do taboleiro unha única vez.
É útil comezar nunha cela poñendo un 1, e sucesivamente ir colocando os naturais 2,3,4,... ata chegar ao 64 (deste xeito, se chegades a un punto sen saída, podedes seguir o rastro do camiño cara atrás). Tamén para comezar é máis sinxelo poñer o 1 nunha esquina do taboleiro. Boa sorte!
No vindeiro post falarei dunha solución sorprendente que deu Euler.
Pero ao nivel que podo comentar neste blog, Euler foi tamén formidable á hora de resolver problemas, tanto "serios" como "lúdicos". É enorme a cantidade de problemas famosos, xogos e paradoxos que foron resoltos por Euler. Antes de comentar algúns, tentade vós resolver un problema dos que tratou este magnífico matemático. Non sei se xa o comentei aquí, pois ás veces mesturo os temas tratados nas aulas e os temas dos que escribo aquí. E nalgunhas clases deste ano do ano pasado si que apareceu o problema. Ao choio:
Movendo ao xeito dun cabalo de xadrez, e comezando nunha cela calquera do taboleiro, tenta pasar por tódalas celas do taboleiro unha única vez.
É útil comezar nunha cela poñendo un 1, e sucesivamente ir colocando os naturais 2,3,4,... ata chegar ao 64 (deste xeito, se chegades a un punto sen saída, podedes seguir o rastro do camiño cara atrás). Tamén para comezar é máis sinxelo poñer o 1 nunha esquina do taboleiro. Boa sorte!
No vindeiro post falarei dunha solución sorprendente que deu Euler.
Etiquetas:
Matemáticos,
Problemas
10.5.10
Quen di que as Matemáticas son inútiles?
Tranquilos que non vou facer unha enumeración de tódalas situacións da vida nas que aparecen implícita ou explicitamente as Matemáticas. Non, hoxe quero amosar que as Matemáticas son útiles do xeito que os alumnos queren ver: o relacionado cos cartos.
Se tedes tempo e ganas, hai unha oportunidade de gañar cartos resolvendo uns problemas relacionados cos cadrados máxicos. Por se alguén non o sabe, un cadrado máxico non é máis que unha táboa cadrada de números na que as sumas de cada ringleira, columna e de cada unha das dúas diagonais é a mesma.
O máis coñecido é o cadrado máxico 3x3:
 onde a suma das 3 ringleiras, as 3 columnas e as 2 diagonais é 15 (cos números do 1 ao 9 non podía ser outra).
onde a suma das 3 ringleiras, as 3 columnas e as 2 diagonais é 15 (cos números do 1 ao 9 non podía ser outra).
Hai moita máis liberdade para elaborar cadrados máxicos se non restrinximos os números aos primeiros números naturais. Por exemplo, o seguinte tamén é un cadrado máxico:

Agora seguro que pensades que é sinxelo crear cadrados máxicos. Resulta máis complicado crear cadrados máxicos suxeitos a certas condicións especiais. Por exemplo, o xenio Leonhard Euler creou o seguinte cadrado máxico 4x4 (con suma 8515):
 Que non semella moi especial, non? Ata que un ve que tódolos elementos son cadrados perfectos:
Que non semella moi especial, non? Ata que un ve que tódolos elementos son cadrados perfectos:
 Curiosamente, Euler atopou este exemplo dun cadrado máxico 4x4 onde tódolos elementos son cadrados perfectos en 1770, sen embargo hoxe en día aínda non se coñece ningún exemplo dun cadrado máxico 3x3 onde tódolos elementos sexan cadrados perfectos, o que a priori parece un problema máis sinxelo.
Curiosamente, Euler atopou este exemplo dun cadrado máxico 4x4 onde tódolos elementos son cadrados perfectos en 1770, sen embargo hoxe en día aínda non se coñece ningún exemplo dun cadrado máxico 3x3 onde tódolos elementos sexan cadrados perfectos, o que a priori parece un problema máis sinxelo.
O cadrado máxico (ata o momento) máis preto de resolver ese problema é o seguinte:

no que tódolos elementos agás dous son cadrados perfectos, e foi a topado por Andrew Bremner.
Volvendo ao tema principal do post, os cartos, o informático Christian Boyer ofrece 1000 € e unha botella de champán por resolver o problema relacionado, en versión "light":
Construír un cadrado máxico 3×3 utilizando sete (ou oito, ou nove) cadrados perfectos distintos que sexa diferente do único exemplo coñecido e das súas rotacións, simetrías e múltiplos k² (dado un cadrado máxico, é sinxelo crear outro multiplicando cada elemento por un cadrado perfecto que escollamos). Ou probar que é imposible.
Tamén ofrece 1000 € e unha botella de champán por outros 5 enigmas principais e cantidades comprendidas entre 100 € e 500 € (máis a botella, que non falte) por outros seis enigmas "menores". A información completa está na súa web, e un resumo neste pdf,
What are the smallest possible magic squares?
Para ser exactos, xa non hai 6 enigmas principais e 6 enigmas menores, pois Toshihiro Shirakawa, de Xapón, resolveu xa o principal #5 e o menor #3a. Así que bulide se queredes os cartos (e o champán).
Se tedes tempo e ganas, hai unha oportunidade de gañar cartos resolvendo uns problemas relacionados cos cadrados máxicos. Por se alguén non o sabe, un cadrado máxico non é máis que unha táboa cadrada de números na que as sumas de cada ringleira, columna e de cada unha das dúas diagonais é a mesma.
O máis coñecido é o cadrado máxico 3x3:
 onde a suma das 3 ringleiras, as 3 columnas e as 2 diagonais é 15 (cos números do 1 ao 9 non podía ser outra).
onde a suma das 3 ringleiras, as 3 columnas e as 2 diagonais é 15 (cos números do 1 ao 9 non podía ser outra).Hai moita máis liberdade para elaborar cadrados máxicos se non restrinximos os números aos primeiros números naturais. Por exemplo, o seguinte tamén é un cadrado máxico:

Agora seguro que pensades que é sinxelo crear cadrados máxicos. Resulta máis complicado crear cadrados máxicos suxeitos a certas condicións especiais. Por exemplo, o xenio Leonhard Euler creou o seguinte cadrado máxico 4x4 (con suma 8515):
 Que non semella moi especial, non? Ata que un ve que tódolos elementos son cadrados perfectos:
Que non semella moi especial, non? Ata que un ve que tódolos elementos son cadrados perfectos: Curiosamente, Euler atopou este exemplo dun cadrado máxico 4x4 onde tódolos elementos son cadrados perfectos en 1770, sen embargo hoxe en día aínda non se coñece ningún exemplo dun cadrado máxico 3x3 onde tódolos elementos sexan cadrados perfectos, o que a priori parece un problema máis sinxelo.
Curiosamente, Euler atopou este exemplo dun cadrado máxico 4x4 onde tódolos elementos son cadrados perfectos en 1770, sen embargo hoxe en día aínda non se coñece ningún exemplo dun cadrado máxico 3x3 onde tódolos elementos sexan cadrados perfectos, o que a priori parece un problema máis sinxelo.O cadrado máxico (ata o momento) máis preto de resolver ese problema é o seguinte:

no que tódolos elementos agás dous son cadrados perfectos, e foi a topado por Andrew Bremner.
Volvendo ao tema principal do post, os cartos, o informático Christian Boyer ofrece 1000 € e unha botella de champán por resolver o problema relacionado, en versión "light":
Construír un cadrado máxico 3×3 utilizando sete (ou oito, ou nove) cadrados perfectos distintos que sexa diferente do único exemplo coñecido e das súas rotacións, simetrías e múltiplos k² (dado un cadrado máxico, é sinxelo crear outro multiplicando cada elemento por un cadrado perfecto que escollamos). Ou probar que é imposible.
Tamén ofrece 1000 € e unha botella de champán por outros 5 enigmas principais e cantidades comprendidas entre 100 € e 500 € (máis a botella, que non falte) por outros seis enigmas "menores". A información completa está na súa web, e un resumo neste pdf,
What are the smallest possible magic squares?
Para ser exactos, xa non hai 6 enigmas principais e 6 enigmas menores, pois Toshihiro Shirakawa, de Xapón, resolveu xa o principal #5 e o menor #3a. Así que bulide se queredes os cartos (e o champán).
Etiquetas:
Aula,
Matemáticos
6.5.10
Cadrados e máis cadrados
Hai moitos problemas clásicos que nunca propoño nas clases ,basicamente por demasiado coñecidos. Problemas de debuxar figuras sen erguer o lapis do papel, de contar triángulos ou outras figuras, o da chalana, o lobo, a leituga e a cabra,... Quizais isto sexa un erro, pois algúns alumnos pode que non vaian coñecer por outros medios estes problemas tradicionais, que adoitan ser bastante divertidos. Para cubrir unha lagoa, hoxe quero propoñer un problema coñecido por tódolos aficionados aos problemas de Matemáticas recreativas:
Cantos cadrados hai nun taboleiro de xadrez?
Obviamente, a resposta non pode ser 64, iso non sería un problema...
Cantos cadrados hai nun taboleiro de xadrez?
Obviamente, a resposta non pode ser 64, iso non sería un problema...
Etiquetas:
Problemas
4.5.10
Now playing!
Desde que adaptei o meu método de ensinanza en 2º de E.S.O. ao clásico: lede en voz alta o libro de texto (e así de paso usámolo para algo ademais dos exercicios mecánicos) curiosamente non noto ningún empeoramento da comprensión. Polo menos tampouco noto ningunha mellora, cousa que si que sería preocupante.
Como teño que estar catro horas á semana artificialmente anoxado nunha clase, non teño moitas ganas de temas serios fóra dela.
E así chegamos aos temas que quero comentar hoxe: xogos.
O primeiro é outro clon máis do Tetris, pero neste caso xogado sobre os lados dun cadrado (e por tanto a figura completa, en troques dun rectángulo, é un ortoedro). Chámase Tetris Cuboid 3D, e é bastante sinxelo, só resulta complicado cando non dá tempo para mover as pezas polas arestas do ortoedro:

Quizais debería crear unha etiqueta especial "Tetris", pois non sei xa cantos xogos baseados no xogo de Alexei Pajitnov terei comentado.
E no outro xogo, Time Paradox, creas copias do personaxe mediante máquinas do tempo que hai pola pantalla de xogo, tendo en conta que eses clons non poden atoparse, como é ben coñecido por tódolos fans da ciencia-ficción. Ademais, o teu personaxe só pode actuar durante 30 segundos, e cada máquina do tempo só pode ser utilizada unha vez, ata que perdas unha vida.
Observade por exemplo como o personaxe está agochado do seu clon nesta captura:

Aínda non xoguei moito ao Time Paradox, espero que os niveis superiores non decepcionen.
E se queredes saber máis do tema, hai un interesante e extenso artigo na wikipedia sobre as viaxes no tempo aquí.
Como teño que estar catro horas á semana artificialmente anoxado nunha clase, non teño moitas ganas de temas serios fóra dela.
E así chegamos aos temas que quero comentar hoxe: xogos.
O primeiro é outro clon máis do Tetris, pero neste caso xogado sobre os lados dun cadrado (e por tanto a figura completa, en troques dun rectángulo, é un ortoedro). Chámase Tetris Cuboid 3D, e é bastante sinxelo, só resulta complicado cando non dá tempo para mover as pezas polas arestas do ortoedro:

Quizais debería crear unha etiqueta especial "Tetris", pois non sei xa cantos xogos baseados no xogo de Alexei Pajitnov terei comentado.
E no outro xogo, Time Paradox, creas copias do personaxe mediante máquinas do tempo que hai pola pantalla de xogo, tendo en conta que eses clons non poden atoparse, como é ben coñecido por tódolos fans da ciencia-ficción. Ademais, o teu personaxe só pode actuar durante 30 segundos, e cada máquina do tempo só pode ser utilizada unha vez, ata que perdas unha vida.
Observade por exemplo como o personaxe está agochado do seu clon nesta captura:

Aínda non xoguei moito ao Time Paradox, espero que os niveis superiores non decepcionen.
E se queredes saber máis do tema, hai un interesante e extenso artigo na wikipedia sobre as viaxes no tempo aquí.
Etiquetas:
Xogos
1.5.10
A estas alturas...
... non debe quedar ninguén no instituto que non saiba que vou liscar o vindeiro ano. Na maior parte dos casos fun eu mesmo quen o comentou nas aulas. Teño que dicir que polo menos en dúas das cinco clases que dou houbo algún alumnos que prefería que non marchase. Isto pode estar motivado esencialmente por dúas razóns: a primeira consiste en que, a pouco máis dun mes de clase, é bastante intelixente dicirlle ao profesor o que quere oír. A segunda é que realmente prefiren que non marche, o cal está relacionado co feito de que lles gusta escoitar as historias que lles conto cando non estamos inmersos no traballo habitual de tódolos días. Porque o meu obxectivo primordial, que era acadar que analicen os problemas, que critiquen as solucións que van aparecendo, que vexan alén dos algoritmos (que veñen marcados por lei, teño que salientar)... digamos que quedou no camiño, deixado de lado pola velocidade do curso e a resistencia dos alumnos a deixar de memorizar procedementos automáticos.
Por outra banda nunha das outras tres clases leva habendo unha especie de rebelión global polo menos durante un mes. Desa clase xa falei en varias ocasións: é a única das miñas cinco clases na que practicamente tódolos alumnos xa foran alumnos meus o ano pasado. E debido á súa conduta, ata que rematemos o curso van ter un exame tódolos xoves. Ademais, é bastante probable que teñan que aprender pola súa conta os contidos que restan, pois é virtualmente imposible ensinarlles nada que leve máis de dez segundos.
Por se alguén non o sabe, na lei educativa en vigor aparece explicitamente a seguinte xoia:
"...sempre debe terse en conta que se reforza a compresión dos contidos matemáticos cando as actividades que teñen que realizar as alumnas e os alumnos están conectadas a contextos do mundo real ou son significativos para eles."
Ninguén aprecia o problema ao que nos enfrontamos? Alguén que coñeza o que resulta significativo para un alumno medio de 13-14 anos?
Deixo o tema, que o único que consigo pensando máis nel é ver que a miña tarefa faise máis e máis complicada (aínda tendo en conta que eu si sei o que lles resulta significativo).
Remato cun vídeo gravado na miña terra. Por se non o sabiades, a praia de Pantín está a metade de camiño entre Ferrol e Cedeira (algo máis preto de Cedeira):
Por outra banda nunha das outras tres clases leva habendo unha especie de rebelión global polo menos durante un mes. Desa clase xa falei en varias ocasións: é a única das miñas cinco clases na que practicamente tódolos alumnos xa foran alumnos meus o ano pasado. E debido á súa conduta, ata que rematemos o curso van ter un exame tódolos xoves. Ademais, é bastante probable que teñan que aprender pola súa conta os contidos que restan, pois é virtualmente imposible ensinarlles nada que leve máis de dez segundos.
Por se alguén non o sabe, na lei educativa en vigor aparece explicitamente a seguinte xoia:
"...sempre debe terse en conta que se reforza a compresión dos contidos matemáticos cando as actividades que teñen que realizar as alumnas e os alumnos están conectadas a contextos do mundo real ou son significativos para eles."
Ninguén aprecia o problema ao que nos enfrontamos? Alguén que coñeza o que resulta significativo para un alumno medio de 13-14 anos?
Deixo o tema, que o único que consigo pensando máis nel é ver que a miña tarefa faise máis e máis complicada (aínda tendo en conta que eu si sei o que lles resulta significativo).
Remato cun vídeo gravado na miña terra. Por se non o sabiades, a praia de Pantín está a metade de camiño entre Ferrol e Cedeira (algo máis preto de Cedeira):
Pantin Classic from Fernando Lema on Vimeo.
Subscribirse a:
Publicacións (Atom)







