Sen máis demora, velaquí:
 |
Seguimos o ano que vén.
"When I use a word... it means just what I choose it to mean"
Sen máis demora, velaquí:
 |
Seguimos o ano que vén.
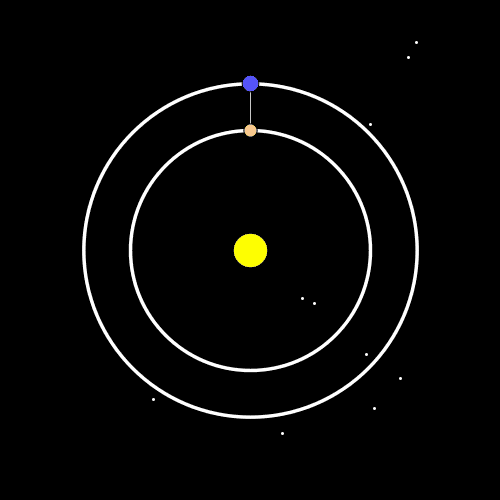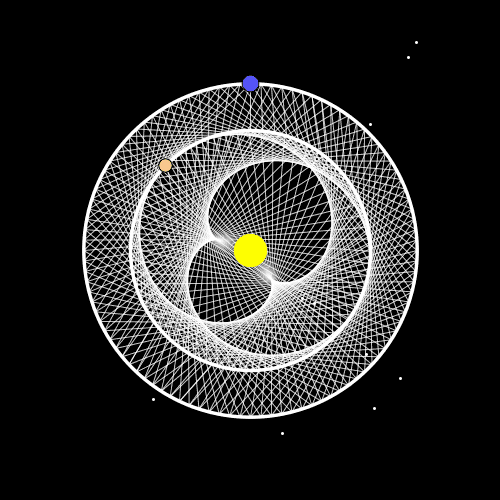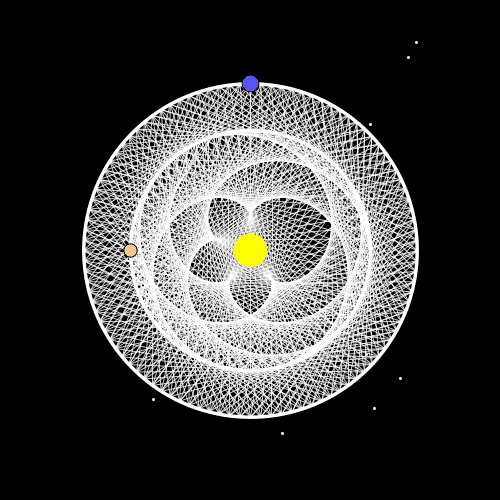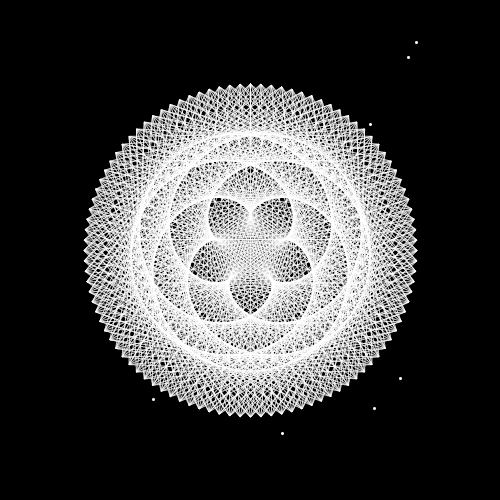
Xogando co geogebra deume por comezar cunha premisa xa manida: a partir da parábola canónica $y=x^2$, coller un punto móbil e fedellar con graos de liberdade(áreas fixas, perímetros fixos, puntos medios, etc.). E atopei un lugar xeométrico que pode que sexa ben coñecido, mais eu nunca vira. Observade.
Partimos da parábola de sempre, co seu vértice $(0,0)$. Collemos un punto móbil P na parábola, e consideramos o segmento que une ese punto co vértice. Nese segmento trazamos a mediatriz, que corta en dous puntos, A e B, á parábola, e fixámonos no punto medio do segmento que une A e B, M.
Que demo de lugar percorre M? Desde logo podemos prever que o seu lugar vai ser simétrico respecto do eixe Y, e tamén o seu comportamento no infinito e nunha veciñanza do 0, pero non contaba coa complicación da súa expresión.
Aínda que teñades máis vista ca min e xa vaticinárades o aspecto do lugar xeométrico, coido que é un bo exercicio de coordenadas, máis se estades un chisco oxidados coma min.Decateime aínda agora de que ao longo dos anos teño compartido uns cantos applets de geogebra, mais non estou certo de que compartise a miña conta en geogebra.org. Velaquí:
Agora o disclaimer.
Non contedes con atopar virtuosismos: non os posúo. Son pragmático en xeral no uso de calquera aplicación, e tamén co geogebra, por moita versatilidade que presente. Hai máis de 15 anos xa usaba Cabri II nas clases, pouco despois comecei de xeito autodidacta (como todos ao principio) co geogebra, asistín a un curso impartido polo grupo Xeodin no 2008, e dous anos despois eu mesmo impartín un curso eu en Valdeorras, co infausto nome de "Xeoxebra na aula", do que hai que responsabilizar á entidade homologadora... Estamos no 2020, e a Consellería é máis neglixente que nunca na formación dos seus docentes, nesta vaga de cursos nin un de geogebra hai.
En Cedeira tamén utilicei geogebra cos alumnos, aínda que cos precarios netbooks Abalar(un saúdo a Plexus, a Coremain e , por suposto, ao Corte Inglés!). Ademais de na clase ordinaria de Matemáticas, puiden dar unha materia de libre configuración de centro na que un dos bloques de contidos trataba exclusivamente o geogebra, como ferramenta científica e de xeito esporádico, tamén artística.
Cos anos a imposibilidade de usalo na aula cos meus alumnos levoume a facer menos cousas. Supoño que o menor ritmo de escritura de entradas tamén influíu, ao compartir menos "divertimentos xeométricos", por exemplo. Vexo aos virtuosos do asunto en twitter facendo cousas fermosas todos os días(outra cousa é se útiles, niso son moi crítico, non o podo evitar), e ademais de faltarme o seu interese e coñecemento, tamén é certo que utilizo o meu "tempo libre matemático" fundamentalmente en atopar e resolver problemas, e en segundo lugar, en ler propostas didácticas. Só en terceiro lugar vén aprender máis matemáticas, e fedellar en software aínda viría despois.
Cando a web de materiais de geogebra era GeogebraTube tiña materiais que creo que desapareceron, moitas das cousas que fago na aula só teñen existencia offline, pero igual algo útil para a aula aínda haberá, como versión mellorada do que levamos escribindo décadas no encerado con xiz. Como mostra de applet feo pero útil, o inevitable sobre a derivada como límite de secantes:
Remexendo na revista Educaçao e Matemática da Associaçao de Professores de Matemática de Portugal, atopei esta pequena xoia elemental:
Temos un quadrado ABCD. Pelos vértices A, B e C traçamos três retas paralelas a, b e c. A distância entre as retas a e b é de 5 centímetros e entre as rectas b e c é de 11 centímetros.
Qual é a área do quadrado?
 |
 |
Xa vai un tempo desde a última entrada na que compartín uns problemas, polo que veño a resolver esta eiva.
O primeiro, da 2º rolda da edición de 2020 do sempre fabuloso concurso Georg Mohr:
 |
| Que ninguén se pregunte por que facemos isto... |
Veña, agora un de contar, que apareceu no Alma Math Challenge do 2018:
$$N=\frac{1}{2} (6n+1)(3n^2+n+2)$$
E para rematar por hoxe, un sinxelo problema xeométrico que apareceu na Olimpíada Finlandesa de 2005, no que a figura é abondo para adiviñar a pregunta:
 |
| Isto pode mellorarse |
 |
| Así mellor |
 |
| Collido do tristemente descontinuo matthen |
 |
| Copiei a imaxe do pdf e chanteina aquí desde o portapapeis, first time ever |
Un dos contidos máis inaccesibles do curriculum de secundaria é o do número real. O positivo é que isto un só o detecta cando aprende máis adiante na súa formación, probablemente en 1º de carreira, que as cousas non son tan sinxelas como lle contaron no instituto. Un alumno con espírito crítico aceptará as propiedades dos números racionais, despois de todo a súa construción é máis ou menos transparente a partir dos números naturais, onde un observa as engrenaxes e por tanto, asimílaas aínda sen ter probas formais de que sexan certas. Pero os irracionais, ai os irracionais, é unha historia totalmente distinta. Xa teño comentado por aquí, seguindo a Hung-Hsi Wu, que facemos trampas ao introducirmos os reais, a súa estrutura e as súas propiedades, aínda as puramente aritméticas, non falemos xa das topolóxicas.
Cando traballamos a forma decimal de números racionais e irracionais, en 3º ou 4º, e falamos de como recoñecer un número irracional vendo o seu aspecto, adoito poñer uns exemplos racionais ben coñecidos:
A unha semana do comezo das clases máis estraño que temos visto, vou compartir unha actividade que fixen no curso 2018/19 coa miña titoría de 3º de ESO. Veredes que, en realidade, a actividade é transportable a calquera curso da ESO ou mesmo 1º de BAC, depende do titor, se quere enfatizar a análise matemática das gráficas ou o diálogo titor-clase.
Para empezar, coñecía a gráfica de xkcd de arriba, na que podemos ver a idea das coordenadas cartesianas de xeito informal. Os eixes non están numerados, non está localizada a unidade, a colocación relativa das froitas só dá unha idea difusa do sinxelo que é comela e do saborosa. Deste xeito, podemos ver que Randall cre que as uvas con sementes son máis difíciles de comer que as uvas sen sementes(aínda que seguen a ser máis sinxelas que difíciles) mais son un chisquiño máis saborosas. Para isto non é necesario indicar a unidade en cada eixe, de feito, habería que dar un significado ao 1 na magnitude "dificultade para comer a froita" E que significado tería -3? E aínda sen unidades, podemos facer preguntas (e esperar respostas coherentes) como "Que teñen en común as mazás verdes e as vermellas? En que se distinguen?"
Pois con esta gráfica na memoria, decidín probar o seguinte: amosei no EDI a imaxe, discutimos un anaco sobre as nosas opinións acerca do sabor e a dificultade(non hai nada como os gustos persoais para que a conversa sexa acalorada), e despois propuxen que cada alumno elaborase nunha cuartilla cadansúa gráfica, cos mesmos eixes que na de xkcd, sinxelo-difícil e non me gusta-gústame e coas materias de 3º de ESO en troques das froitas. Velaquí algunhas das producións:
La paradoja del niño o niña: aplicaciones para la clase de probabilidad
En troques, pelexade coas seguintes cuestións, tamén clásicas mais, coido, non tan coñecidas:
Imaxinade que temos unha baralla composta polo as de espadas, os as de copas, o dous de espadas e o dous de copas.
1ª cuestión: extraemos dúas cartas desa baralla. Cal é a probabilidade de que nesa man saian os dous ases, se sabemos que saíu polo menos un as?
2ª cuestión: extraemos dúas cartas desa baralla, one more time. Cal é a probabilidade de que nesa man saian os dous ases, se sabemos que saíu o as de espadas?
E cando os resolvades, tedes outro choio: que diferencia esta parella de cuestións da parella de cuestións mencionada ao comezo?
 | ||
|
 |
| A xeometría non euclidiana da foto non é como a das que mandaban os alumnos no confinamento, que isto é un libro |
 |
| Que conste que vén sendo tan rigorosa como outras aparicións de φ que se ven por aí... |

Por que é tan famoso este ítem?
Porque, como conta Howard Eves no seu libro Return to Mathematical Circles, o comité que creara o ítem deu por boa unha resposta incorrecta. E isto non se soubo ata que un rapaz de 17 anos, Daniel Lowen, atopou a resposta correcta e foi teimudo abondo para non admitir que lle desen por mal a súa resposta. Ata que o seu pai se puxo en contacto co Educational Testing Service
O voso choio consiste en dúas tarefas: 1º) atopar a resposta correcta e 2º) adiviñar cal era a resposta incorrecta que o comité dera por válida, e por que.
|
| a) $2$ | b) $\frac{1}{2}$ | c) $9$ | d) $-3$ |
|---|
 |
| Par+Impar=Par? Descansa, Wiles. |
 |
| E se as diagonais non se cruzan? |
 |
| Que facíamos os profesores antes da existencia do Geogebra 3D? |
 |
| O que parece coincidir, coincide |
 |
| Aquí ademais as pezas son iguais, aínda que ninguén o pedía |
 |
| Xuraría que o primeiro xa anda por este blog |