A raíz de 2 é irracional, disque

 

Doce anos leva en liña este blog de Matemáticas... e aínda non compartín ningunha demostración da irracionalidade de 2? Algún día había que arranxar isto (deixamos para outro día o de comentar algo do cubo de Rubik, origami ou xadrez).

Para resaltar o elegante que é a demostración que vou compartir, vexamos antes outras demostracións máis tradicionais ou escolares, comezando pola que se facía nas clases de BUP.

• Supoñamos, por redución ao absurdo, que $\sqrt{2} \in \mathbb{Q}$. Daquela hai naturais a e b coprimos(pois sempre podemos simplificar a fracción ata chegar á irredutible) que cumpren que $\sqrt{2} = \frac{a}{b}$. Elevando ao cadrado, $2=\frac{a^2}{b^2} \rightarrow 2b^2=a^2$ (1). Desta igualdade deducimos que a² é par, o que implica que a é par(podemos poñernos máis ou menos pedantes neste paso), de onde $\exists k \in \mathbb{N} / a=2k$. Substituímos o valor de a: $2b^2=(2k)^2 \rightarrow 2b^2=4k^2 \rightarrow b^2=2k^2$, e de xeito análogo, deducimos que b² é par, polo que b é par, e a fracción $\frac{a}{b}$ é irredutible, en contra da hipótese, polo que concluímos que $\sqrt{2} \notin \mathbb{Q}$

A demostración anterior, que si aparecera neste blog, nunha foto dos meus vellos apuntamentos de 1º de BUP, admite variantes, todas xogando coa mesma idea:

• En (1) podemos razoar de xeito máis elegante do seguinte xeito. Observemos os dous membros da igualdade, $2b^2=a^2$. E fixémonos na aparición do primo 2 na descomposición en factores primos de cada membro. O da dereita, sendo un cadrado, ten un expoñente par en todos os seus factores, incluído o 2. O da dereita, ao ser o dobre dun cadrado, vai ter un expoñente par en todos os seus factores primos agás o 2, no que terá un expoñente impar. E un número non pode ser par e impar á vez. Chegamos ao absurdo outra vez. 

Se en troques de incidir na irredutibilidade da fracción que representa $\sqrt{2}$, incidimos no carácter minimal de, por exemplo, o seu denominador, obtemos outra familia de demostracións. Explico mellor: se $\sqrt{2}$ pode ser expresado como o cociente de dous números naturais, haberá unha fracción entre todas as posibles representantes que teña o menor denominador. Esa fracción terá carácter minimal. E levar esta idea ao campo da xeometría é moi frutífero.

Pero antes, unha demostración no campo das fraccións continuas, un deses campos elementais que non están moi de moda:

• Observando que $\left( \sqrt{2}-1\right)\left( \sqrt{2}+1\right)=\left( \sqrt{2}\right)^2-1^2=2-1=1$, reescribimos como $\sqrt{2}-1=\frac{1}{1+\sqrt{2}} \rightarrow \sqrt{2}=1+\frac{1}{1+\sqrt{2}}$. E agora iteramos o proceso de substituír $\sqrt{2}$ $\sqrt{2}=1+\frac{1}{1+\sqrt{2}}=1+\frac{1}{1+1+\frac{1}{1+\sqrt{2}}}=1+\frac{1}{2+\frac{1}{1+\sqrt{2}}}$ $1+\frac{1}{2+\frac{1}{2+\frac{1}{1+\sqrt{2}}}}=1+\frac{1}{2+\frac{1}{2+\frac{1}{2+ \dots}}}$

O proceso non remata, é dicir, a fracción continua é infinita, e como todos os racionais teñen unha fracción continua finita, deducimos que o número representado é irracional. Na notación tradicional para a representación en fracción continua, $\sqrt{2}=\left[1;2,2,2, \dots \right]$

Vaiamos coa primeira demostración xeométrica que coñecín, hai xa uns lustros, da man do famoso teórico de números Tom Apostol(famoso principalmente por ter un libro de Cálculo Infinitesimal na bibliografía de 1º de carreira en todo o mundo).

• A estratexia de demostración mencionada previamente chámase "por descenso infinito", forma parte da caixa de ferramentas da Teoría de Números e a nivel elemental, da resolución de problemas de olimpíadas. Neste caso concreto, partimos dun triángulo rectángulo isóscele con lados naturais m e n, polo que $m^2=2n^2$, e imos amosar que sempre hai outro triángulo rectángulo isóscele con lados naturais e máis pequenos.

Aritmeticamente, $2(m-n)^2=(2n-m)^2$

Trazamos a circunferencia de centro C e radio n, e marcamos o punto no que corta á hipotenusa, D. Debuxamos a perpendicular á hipotenusa que pasa por P, e marcamos o punto no que corta ao cateto AB, E. Pois ben, o triángulo DEB é rectángulo, isóscele e ten lados enteiros, e obviamente ten lonxitudes menores que as de ABC, co cal iniciamos o descenso: sempre hai outro triángulo coas características atribuídas. O descenso está totalmente intricado co a redución ao absurdo, vén sendo como unha versión: se supoñemos que hai un triángulo minimal con esas características, chegamos ao absurdo, pois o descenso amosa que vai haber outro.

Agora que xa coñecemos esta estratexia, vexamos outra demostración totalmente distinta desde o punto de vista xeométrico pero que utiliza o mesmo metaargumento. Esta demostración foi popularizada polo xenial John H. Conway, mais o creador foi Stanley Tennenbaum, lóxico matemático.

• Partamos agora da existencia de dous números n e m tales que $m^2=2n^2$, i.e, $m^2=n^2+n^2$, e explotemos a representación automática destas cantidades como áreas de cadrados.

Metamos os dous cadrados pequenos no grande:

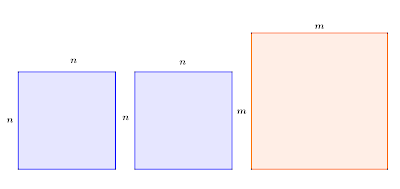Intuídes cara onde imos?

Os dous cadrados pequenos solápanse formando outro cadrado máis pequeno. E deixan fóra dous cadrados laranxas na figura, que son iguais entre si. Reparemos neles:

Aínda que poderíamos apelar simplemente ao Teorema das Alfombras, o razoamento directo é inmediato: como a área do cadrado laranxa orixinal coincide coa dos dous cadrados lilas, o que sobresae por fóra dos cadrados ten que coincidir coa zona solapada, na última figura, o cadrado verde e os dous vermellos. Deste xeito habilitamos o descenso buscado: hai cadrados máis pequenos que cumpren a condición de que a área do grande é igual á suma da área dos dous pequenos e iguais.

Coido que vou deixar aquí esta compilación de demostracións, para non cansar ao amable lector. Quizais outro día, antes de que pasen 12 anos, retome a xeira.