Analítica & sintética

 Debido á precaria ensinanza da Xeometría na época da EXB e a New Math, eu padecín dous fenómenos: por unha banda a xeometría sintética reduciuse a unha breve nomenclatura xunto a unha listaxe de fórmulas de áreas, esencialmente, e por outra a xeometría analítica aparecía no BUP totalmente desconectada da pouca sintética que se vira antes. Hai que recoñecer que, aínda que agora se dea algo mellor a xeometría sintética que daquela, o salto entre as dúas perspectivas no estudo dos obxectos xeométricos é ben amplo. Quizais, por buscar unha analoxía, suceda algo semellante no estudo a finais de bacharelato da xenética clásica e da xenética molecular en Bioloxía, cuxa conexión desde logo non aprendín facendo COU.

Se hai algún ámbito no que as dúas visións da xeometría teñen intersección, seguramente sexa a trigonometría, que comeza sendo puramente sintética, con triángulos flotando no limbo, e remata apoiándose nas coordenadas simplemente para ampliar o estudo dos ángulos agudos a ángulos calquera.

E se segue a haber un ámbito no que é difícil que o alumnado vexa a conexión coa xeometría sintética é, como apuntei arriba, o da xeometría analítica das rectas, que se comeza en 4º de ESO e continúa en Matemáticas I. Por iso eu levo uns anos introducindo exercicios nos que as cuestións elementais de xeometría sintética teñen consecuencias no contexto dos vectores no plano. Sinceramente non foi unha idea que xurdira da reflexión sobre a miña docencia, senón que xurdiu casualmente mirando uns libros do IGCSE de Cambridge, cando atopei uns exercicios deste estilo:

De paso aí vai o uso de 1:3 para indicar a razón, tan pouco visto en España

Nese momento descubrín que nos exames estandarizados dos países anglosaxóns é habitual atopar problemas nos que hai que dominar a maquinaria dos vectores pero simultaneamente hai que utilizar semellanza de triángulos, congruencia, paralelismo de rectas e segmentos alén do trivial, etc. Velaquí unha escolma de problemas inusuais para o que estamos acostumados nós(aquí falo como se soubese que fai cada profesor na súa aula, permitídeme a licenza).

Xa é raro ver un segmento bailando

GCSE(9-1) Paper 3(Calculator) 2017

OAN, OMB a APB son liñas rectas.

$AN=2=OA$

M é o punto medio de OB.

$\vec{OA}=a, \vec{OB}=b$

$\vec{AP}=k \vec{AB}$, onde k é unha cantidade escalar.

Dado que MPN é unha liña recta, atopar o valor de k 

GCSE(9-1) Paper 1(Non-Calculator) 2017

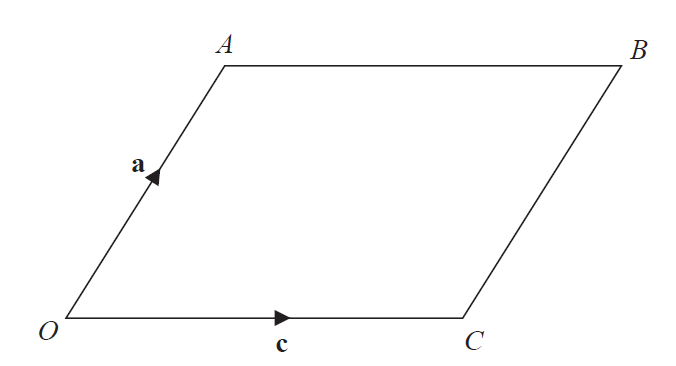
OABC é un paralelogramo

$\vec{OA}=\textbf{a}, \vec{OC}=\textbf{c}$

X é o punto medio da liña AC.

OCD é unha liña recta na que $OC:CD=k:1$

Dado que $\vec{XD}=3\textbf{c}-\frac{1}{2} \textbf{a}$, atopar o valor de k.

GCSE(9-1) Paper 1(Non-Calculator) 2018

OAB é un triángulo.

OPM e APN son liñas rectas.

M é o punto medio de AB

$\vec{OA}=\textbf{a}, \vec{OB}=\textbf{b}$

$OP:PM=3:2$

Calcula a razón $ON:NB$

GCSE Mathematics B Unit 3: Number, Algebra, Geometry 2(Calculator) 2014

OABC é un paralelogramo.

M é o punto medio de AC.

C é o punto medio do segmento BCX.

$\vec{OA}=\textbf{a}, \vec{OB}=\textbf{b}$

Demostrar que OMX é unha liña recta.

E aínda que non aparezan vectores, non podo deixar pasar a ocasión de compartir outro problema de xeometría no que interveñen feitos básicos e razoamento:

GCSE(9-1) Paper 3(Calculator) 2018

ABCD é un paralelogramo.

ABP e QDC son liñas rectas.

$\angle{ADP}=\angle{CBQ}=90^{\circ}$

a) Demostrar que o triángulo ADP é congruente ao triángulo CBQ.

b) Explicar por que AQ é paralelo a PC

Remato poñendo a ligazón oficial de Pearson onde podedes descargar os exames e as rúbricas de corrección de calquera materia e exame estandarizado:

Past Papers

E unha ligazón que atopei pola rede onde tedes os pdfs á vista, e instalando unha extensión no navegador poderedes descargar dunha soa vez:

SaveMyExame- Edexcel GCSE Maths: Past Papers