Quen tiña unha hora libre e pensou "veña, vou mirar algún problema do Torneo das Cidades"?
Efectivamente, o voso amigo, que parece novato. Catorce anos pasaron desde a entrada Primeiro Problema dun Libro, dous desde Un Problema do Tournament of the Towns, un feixe desde que sei dos problemas para nenos de Vladimir I. Arnold, e nada, aínda non aprendín que achegarse de xeito inocente a problemas de competicións ou libros rusos nunca sae como un espera inicialmente.
En troques de compartir o problema co seu enunciado orixinal, fagamos unhas cantas liñas.
Partimos dunha circunferencia, que dividimos en oitavos do xeito habitual:
 |
 |
 |
 |
| Prometo que foi ao chou que saíse o diámetro vertical (total, só había 4 opcións) |
Probemos con outra numeración dos mesmos sectores:
 |
Podedes probar vós con calquera outra coloración e calquera outro xeito de numerar os sectores seguindo esas regras. Sempre ides obter dous semicírculos cos números do 1 ao 4.
Pero xa imaxinaredes que esta non é unha propiedade peculiar do 4. Podemos dividir o círculo en 16 sectores, e veremos que sucede o mesmo co número 8. Poñamos novamente un exemplo:
 |
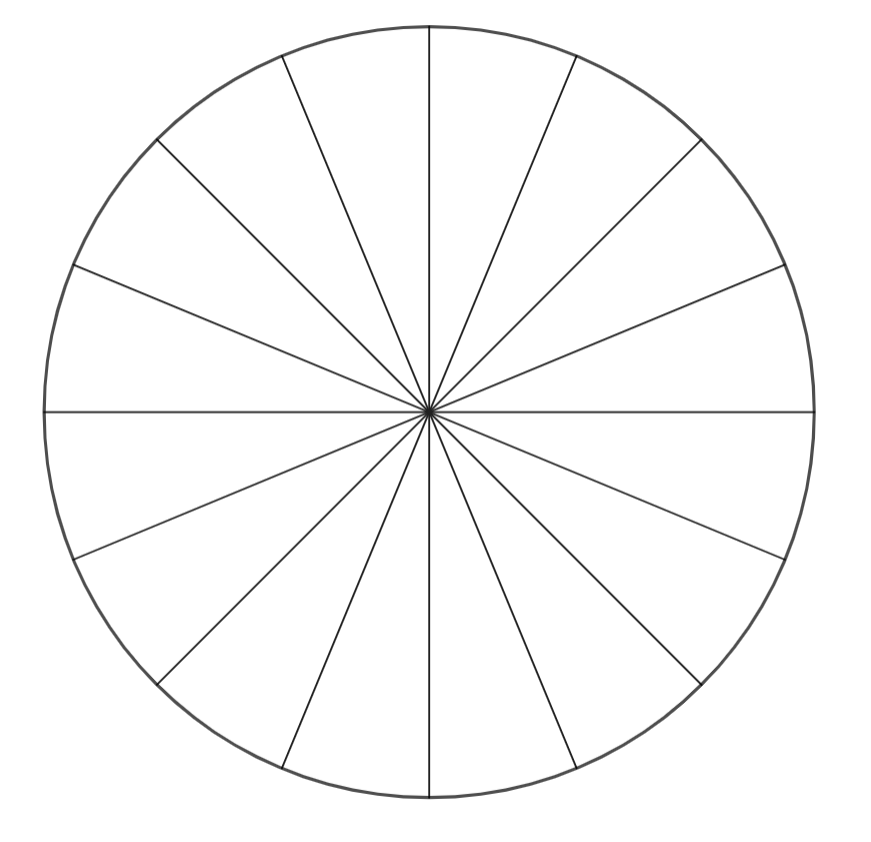 |



Xenial coma sempre.
ResponderEliminarA ver, se algún mérito teño, seguramente sexa o de ler moito. O demais vén rodado.
Eliminar