O cuarto problema da Olimpíada deste ano trataba de números e divisibilidade baixo unha apariencia inocente:
Problema 4
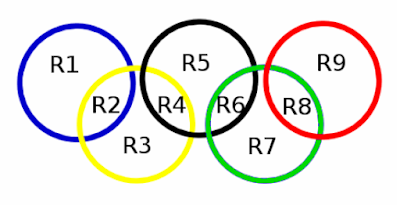
Os aros olímpicos entrelazados determinan 9 rexións diferentes como se indica na imaxe. Encontra 9 números, un en cada rexión, de tal forma que:
- O produto deses números dean, en cada aro, 5 números consecutivos.
- Un deses números consecutivos é o 58.
- Os números non teñen por que estar ordenados de menor a maior.
 |
| Collido (outra vez) de AGAPEMA |
Para resolveren este problema nun tempo razoable(o método de proba-erro ás toas non sería factible no tempo previsto), os cativos tiñan que ter moi claras as peculiaridades dos números primos. Atendendo ás Matemáticas necesarias para resolvelo, coido que este foi o meu problema favorito desta quenda.



0 comentarios:
Publicar un comentario